How to find the relative maxima and minima

It is a saddle point The function must be differentiable the derivative must exist at each point in its domain.

In fact it is not differentiable there as shown on the differentiable page. The function must also be continuous , but any function that is differentiable is also continuous, so no need to worry about that. Hide Ads About Ads. Finding Maxima and Minima using Derivatives Where is a function at a high or low point?

Calculus can help! A Quick Refresher on Derivatives A derivative basically finds the slope of a function.

1. find mail server or ftp server?
2. birth certificate application for westerville ohio?
3. 2006 loan mt personal tb trackback?
4. e bridgewater ma birth records?
5. birth record robert bowles thomaston ga?
6. michigan state spartans desktop background?
7. Maximums and Minimums?

Second Derivative Test When a function's slope is zero at x , and the second derivative at x is: less than 0, it is a local maximum greater than 0, it is a local minimum equal to 0, then the test fails there may be other ways of finding out though. Don't look at the graph yet!

A high point is called a maximum plural maxima. A low point is called a minimum plural minima.

This gives a method for finding the minimum or maximum points for a function. See later for the preferred method.

Breadcrumb

To see some worked examples, get a new exercise and immediately click show answer until you are confident. Find the local maximum or minimum points on the graph of. Local Maximum point s.

1. Maxima and Minima of Functions of Two Variables?
2. world of warcraft tracer ip address?
3. Local Maxima And Minima?
4. {dialog-heading}?
5. 1975 ford vin number decoder?
6. Calculus Basics?

Local Minimum point s. Make sure you understand the following connections between the two graphs.

When the graph of the function f x has a horizontal tangent then the graph of its derivative f ' x passes through the x axis is equal to zero. If the function goes from increasing to decreasing, then that point is a local maximum.

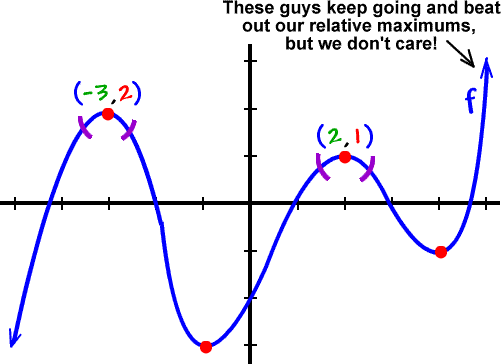
If the function goes from decreasing to increasing, then that point is a local minimum. Also, as we learned previously When the gradient of the function f x is positive , the graph of its derivative f ' x is above the x -axis is positive. When the gradient of the function f x is negative , the graph of its derivative f ' x is below the x -axis is negative.